¿Responder al azar, mejora los puntajes de la PSU?

Algunos días atrás tuve una interesante conversación con mi padre, el profesor de matemática, Danny Perich C. me comentó que algunos colegas suyos, debido a la decisión del DEMRE de eliminar el descuento por respuestas incorrectas, estaban sugiriendo a sus alumnos elegir una alternativa al azar para responder las preguntas de la PSU que no conozcan; por ejemplo, la alternativa (c).

El razonamiento es simple. Si un alumno responde una pregunta al azar, tendrá un 20% de probabilidades de acertar debido a que cada pregunta tiene cinco alternativas. Por ejemplo, si un alumno responde correctamente 35 de las 75 preguntas de la PSU de matemática y el resto al azar, probablemente obtendrá 8 correctas adicionales.

Lo que la gran mayoría no sabe es que si todos los alumnos respondieran al azar las preguntas que no son capaces de resolver, se generaría un efecto negativo gigantesco sobre los puntajes. Para mostrar cómo opera este efecto, es fundamental saber, en primer lugar, cómo se calculan los puntajes de la PSU (CRUCH 2014).

El primer paso consiste en agrupar el número de respuestas correctas según la cantidad de alumnos que han obtenido el mismo número de aciertos o, en términos técnicos, determinar la frecuencia de la cantidad de respuestas correctas.

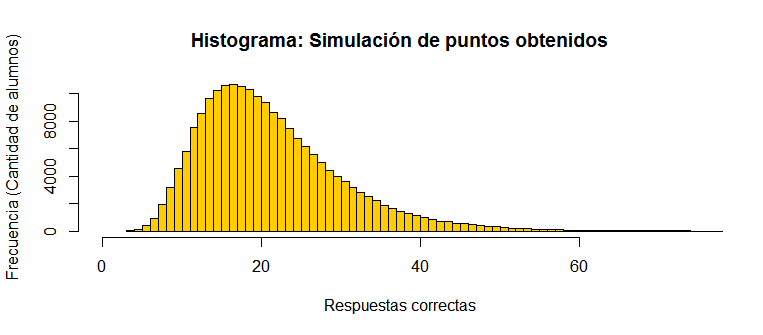
Fuente: Propia. Datos simulados en lenguaje R, con distribución LogNormal de media ln(20) y desviación estándar ln(1,5).

Una vez determinada la frecuencia se procede a la Normalización. Este proceso consiste en el ajuste de la frecuencia de las respuestas correctas a una curva normal (cuya forma es la conocida Campana de Gauss) utilizando una media de 500 y una desviación estándar de 110. En términos simples, una media de 500 puntos implica que un 50% de los alumnos se ubicará tanto por debajo como por encima de ese puntaje; una desviación estándar de 110 implica que un 68% de los alumnos se situará entre los puntajes 390 y 610 puntos, mientras que el 95% lo hará entre los puntajes 280 y 720. Gráficamente:

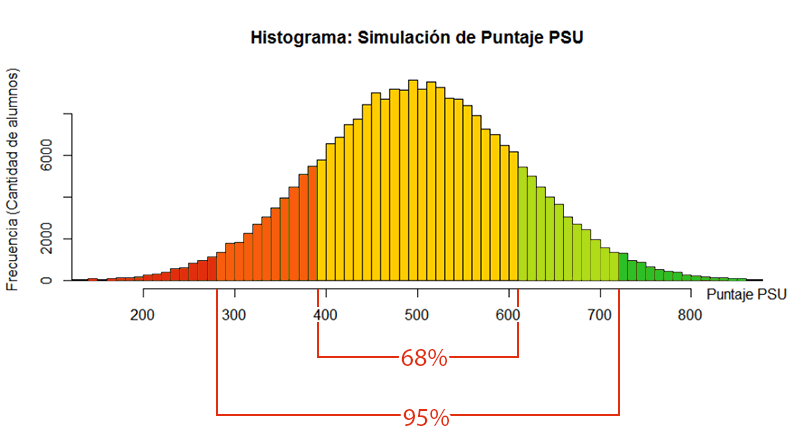
Fuente: Propia. Utilizando los datos simulados, se calculó la probabilidad cumulativa de cada respuesta y se ajustó a una curva normal mediante la fórmula 110x+500.

Una vez que los datos han sido normalizados, se establece una relación funcional entre el número de respuestas correctas y el puntaje PSU. A partir de esta relación, el DEMRE crea unas tablas que muestran la equivalencia entre el número de respuestas correctas (denominado “Puntaje Corregido” o “PC”) y el puntaje final (denominado “Puntaje Estándar” o “PS”).

Gráficamente, la PSU de Matemática presentó la siguiente relación entre el Puntaje Corregido y el Puntaje Estándar para el Proceso de Admisión 2014 (DEMRE 2014-I):

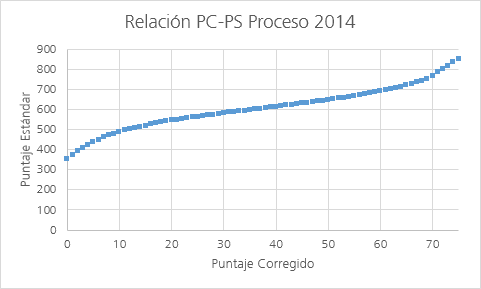
Fuente: Propia. Elaborado con datos provistos por el DEMRE. El 0,5% de los datos correspondientes a las colas izquierda y derecha son ajustados linealmente por el organismo.

Asumamos por un momento que todas las preguntas efectivamente contestadas de un alumno han sido certeras, omitiendo el resto. ¿Cuántas respuestas correctas debería tener un alumno para obtener 850, 700, 600, 500 o 450 puntos? La siguiente tabla resume los Puntajes Corregido y Estándar para estos valores:

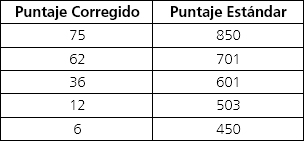
Fuente: Tabla de Transformación de Puntaje Corregido a Puntaje Estándar, DEMRE.

Puede parecer sorprendente que a un estudiante le baste contestar apenas 36 de las 75 preguntas para obtener 600 puntos en la PSU de Matemática. Además, considerando que el 50% del universo se ubica por debajo de los 500 puntos, es aún más sorprendente que el número de respuestas correctas necesarias para obtener este puntaje haya sido apenas de 12.

Insólito resulta el caso de los 450 puntos. Los alumnos de la Universidad del Mar, la Universidad SEK, la UCINF o la Universidad Bernardo O’Higgins, cuyos puntajes promedio oscilan alrededor de los 450 puntos (Perich 2014), habrían contestado correctamente apenas 6 de las 75 preguntas (o bien, el puntaje corregido, una vez descontadas las respuestas incorrectas habría sido apenas de 6).

Lo anterior es una consecuencia de la combinación entre el proceso de normalización y la alta tasa de omisión. Hasta el Proceso de Admisión 2014, los Puntajes Corregidos se concentraban en la parte baja del histograma; debido a que el ajuste a una curva normal “mueve” estos puntajes hacia derecha, a lo largo de los años se creó un incentivo hacia la omisión que, en las pruebas de Matemática y Lenguaje, alcanza el 41% y 25% respectivamente (Bravo et al. 2012). En condiciones normales, si un alumno respondiera correctamente el 50% de las preguntas, sería razonable esperar que obtenga el puntaje promedio; hasta el Proceso de Admisión 2014, bastaba responder correctamente cerca de un 15% de las preguntas para obtener este puntaje.

Existe, además, una razón de fondo por la cual el sistema de descuento es pernicioso. Si bien, algunos alumnos tienen el talento y las capacidades para obtener los máximos puntajes de cada prueba, todo alumno tiene el derecho de equivocarse al responder a una pregunta. Cuando se castigan las incorrectas y no se castiga la omisión, el mensaje que estamos entregando implícitamente es que es mejor no atreverse que equivocarse. ¿Cómo podríamos aspirar a ser un país desarrollado, emprendedor o innovador si castigamos a quien se atreve y premiamos a quien no lo hace?

Con el fin de corregir la distorsión provocada por la alta tasa de omisión de las pruebas (Pearson 2013), el Consejo de Rectores decidió no seguir aplicando el descuento por respuestas incorrectas. Según los modelos de prueba entregados por el DEMRE este año, la obtención de 500 en las nuevas pruebas se obtendría con 20 respuestas correctas en Matemática y 35 en la prueba de Lenguaje.

A partir de estos datos, podemos graficar la relación entre las respuestas correctas y el puntaje esperado en la prueba de Matemática para el Proceso de Admisión 2015 (DEMRE 2014-II):

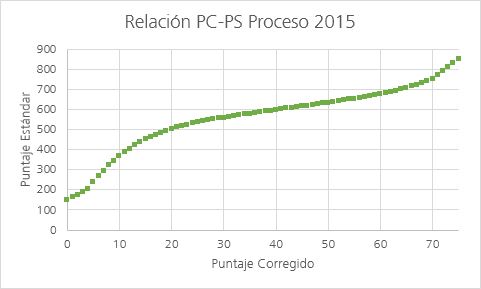
Fuente: Propia, elaborado con datos publicados por el DEMRE

Cuando se castigan las incorrectas y no se castiga la omisión, el mensaje que estamos entregando implícitamente es que es mejor no atreverse que equivocarse. ¿Cómo podríamos aspirar a ser un país desarrollado, emprendedor o innovador si castigamos a quien se atreve y premiamos a quien no lo hace?

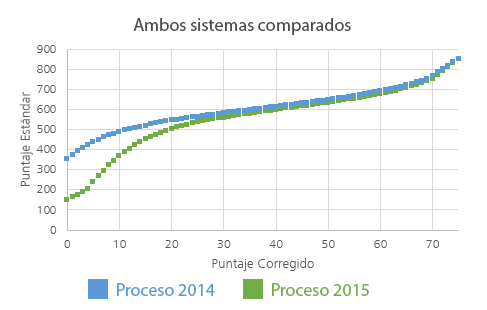
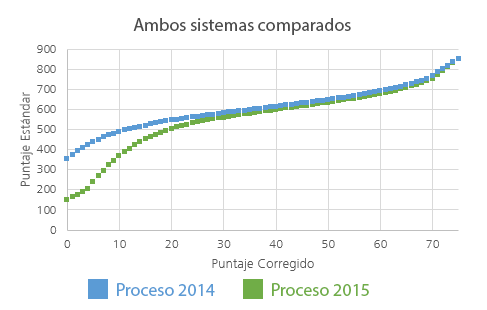
Si superponemos la relación funcional entre el Puntaje Corregido y el Puntaje Estándar para los Procesos de Admisión 2014 y 2015, podemos apreciar claramente que se elimina el “premio” a la omisión:

Lamentablemente, existe un desconocimiento generalizado sobre cómo opera el mecanismo de asignación de puntajes. Y es natural. Es de sentido común asumir que una gran parte de la población desconoce el proceso de normalización que se realiza en los puntajes; al mismo tiempo parece poco razonable exigir que toda la población sepa de estadística como para deducir de qué manera este proceso afecta a los puntajes globales.

Debido a lo anterior, es común leer en distintos medios que, al no castigarse las respuestas incorrectas, los alumnos tendrían la oportunidad de “adivinar”. Esta crítica es absolutamente infundada.

En las siguientes tablas se aprecia comparativamente el número de respuestas al azar que deberían ser correctamente respondidas en la PSU Matemática del Proceso de Admisión 2015 para obtener el mismo puntaje que en la prueba anterior. Para el cálculo, se consideró un 20% de probabilidades de acertar:

Elaboración propia.

Elaboración propia.

Analicemos el caso más extremo ¿Qué sucedería si todos los alumnos del país toman la decisión de responder la alternativa (c) para todas las preguntas que no pueden resolver?

En este caso, el proceso de normalización actuaría de forma mucho más acentuada, disparando hacia abajo los puntajes. El siguiente gráfico muestra cuál sería el efecto de responder (c) en todas las preguntas cuya respuesta se desconoce:

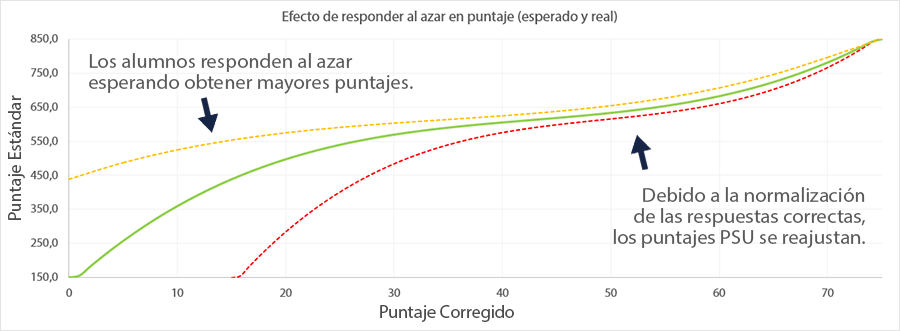
Fuente: Propia, reajustando los datos del DEMRE a funciones polinómicas continuas de grado 3 mediante máxima verosimilitud, manteniendo y cambiando la distribución de percentiles según la cantidad de respuestas correctas, respecto de la función original.

La curva de color verde muestra la relación entre el Puntaje Corregido y el Puntaje Estándar proyectado para la PSU Matemática del Proceso de Admisión 2015. La curva amarilla muestra el puntaje esperado por los alumnos al responder al azar. Este puntaje se obtendría si y sólo si se mantiene la distribución proyectada por el DEMRE.

Sin embargo, debido al proceso de normalización, los puntajes se reajustan completamente. La curva roja muestra cuál sería el resultado si todos los alumnos decidiesen responder al azar. En términos simples, con la proyección para el Proceso de Admisión 2015, sin respuestas al azar, un alumno que tiene todas las respuestas incorrectas (o que omite la totalidad de la prueba) obtendría el mínimo puntaje, es decir, 150. Si todos los alumnos decidieran responder la alternativa (c) en vez de omitir, el puntaje corregido mínimo sería igual a 15; pero debido al reajuste, seguirían obteniendo el mínimo puntaje, es decir, 150; a partir de ahí, los Puntajes Estándar seguirían la proyección de la línea roja.

Es importante aclarar algo. Bajo el nuevo sistema, los alumnos que intenten responder una pregunta apelando a sus conocimientos siempre estarán en ventaja por sobre quienes deciden responder al azar. Además, bajo esta nueva modalidad se podrá medir de mejor manera cuál es el verdadero nivel de conocimientos adquiridos durante la enseñanza media; hasta la última versión de la PSU, esto era imposible de realizar (Pearson 2013).

Por último, quisiera recalcar algo que, en mi opinión, es lo más importante de esta nueva modalidad. Aquellos alumnos que, osadamente, intenten responder una pregunta de la que no están seguros, quizá se equivoquen. Pero ese es exactamente el espíritu de la Universidad. Defender el derecho de sus alumnos a usar el pensamiento incluso a riesgo de equivocarse, pues nuestro mundo se ha construido en base a una incontable cantidad de errores que han cambiado la historia. Newton afirmó que la gravedad era una fuerza y se equivocó; Einstein propuso una constante cosmológica para explicar un universo estático y se equivocó. ¿Qué sería de las ciencias si estos grandes hombres no se hubiesen equivocado? Siempre que el error provenga del pensamiento y no del azar podemos esperar lo mejor para todos nosotros. Tal como dijo Hipatia de Alejandría, “defiende tu derecho a pensar, porque incluso pensar de manera errónea es mejor que no pensar”.

Referencias:

Bravo, D.; Manzi, J.; Silva, I. 2012. “Proceso de Admisión 2012: Antecedentes Y Resultados”. Consejo de Rectores de las Universidades de Chile.
Perich, D. 2014. “Nivel de exigencia académica de las universidades chilenas”.
Consejo de Rectores de las Universidades de Chile CRUCH. 2014. «Normas y Aspectos Importantes del Proceso de Admisión». Documento Oficial Nº 1, años 2014.
Departamento de Evaluación, Medición y Registro Educacional DEMRE. 2014-I. «Tabla de Transformación de Puntaje Corregido a Puntaje Estándar».
Departamento de Evaluación, Medición y Registro Educacional DEMRE. 2014-II. «Modelo de prueba de Matemática». Santiago.
Pearson. 2013. «Informe Final Evaluación de la PSU Chile».